Figure Tpgy.01 - Topology Graph Hierachy

|
Project:
|
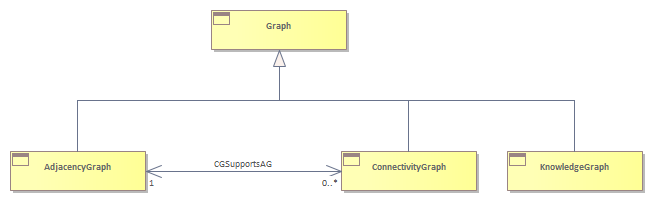
Figure Tpgy.01 - Topology Graph Hierachy : SID diagram
Graphs are a generalized (mathematical) model for defining topologies in terms of logical entities called Vertices and the relationships between them called Edges [ ref Topological graph theory - Wikipedia ]<br/>For the Communications Industry, two practical specializations of graphs are commonly used:<br/>Adjacency Graph - A Graph expressing an adjacency requirement or property, independently of how this is realized (which would be expressed using a Connectivity Graph).<br/>Adjacency is defined as the ability for a set of entities to communicate [TR 244 ]<br/>Connectivity Graph -A Graph expressing the realization of adjacency [TR 244 ]<br/>Knowledge Graph. As OSS and BSS start to incorporate AI, Knowledge graphs are created for capturing the relationships between customers’ products, services, and resources including network. Knowledge Graphs can be modelled as a specialization of mathematical graph but with a broader set of relationship types than is typical in network topology graphs.<br/>References:<br/>Further description and examples of network topology graphs are available in <br/><ul>
<li>TR255A Connectivity Patterns for Virtualization Management v4.0.1 | TM Forum</li></ul> <ul> <li>TR244 TM Forum Information Framework Enhancements to Support ZOOM R15.0.1 | TM Forum</li></ul> These are explained further after the introduction to mathematical graphs.<br/> |




