Figure Tpgy.02 - Mathematical Graph Representation of Topology

|
Project:
|
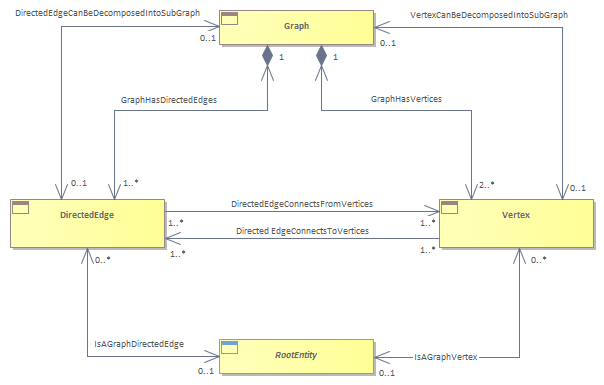
Figure Tpgy.02 - Mathematical Graph Representation of Topology : SID diagram
Graphs are a generalized (mathematical) model for defining topologies in terms of logical entities called Vertices and the relationships between them called Edges [ ref Topological graph theory - Wikipedia ]<br/>Graphs modelled in the Information framework are shown as collection of Vertices and edges that hold the relationship between them. In this model both Vertices and Edges are Rooted on the RootEntity. In mathematical graphs each relationship edge is between two vertices and is directed.<br/>In graphs representing networks, it is common to layer topology graphs each representing a different abstraction each supporting different operational needs. For example a Directed Edge in a network topology linking two routers may represent a communication path which may be further decomposed into a more detailed topology of into edges and vertices representing transmission links, interconnection nodes, multiplexers, etc. The first topology view might support IP Operations needs, whereas the second might represent the assets needed by Transmission Operations to locate faults. This ability to segment and layer graphs, whilst maintaining the linkages among them, makes the topology graph a highly effective tool for supporting operations. <br/>The Information Framework model for graphs has arisen from work in several exemplar studies which derived the model shown above.<br/>
|




